Хань живет в общей квартире. Там живет \(n\) человек (включая Ханя), у каждого из которых есть собственный холодильник.
\(n\) холодильников защищены несколькими цепями. Каждая цепь соединяет два различных холодильника и защищена цифровым замком. Владелец холодильника знает коды доступа всех связанных с ним цепей. Холодильник может быть открыт только в том случае, если все цепи, подключенные к нему, разблокированы. Например, если холодильник вообще не имеет связанных с ним цепей, то его может открыть любой из \(n\) человек.
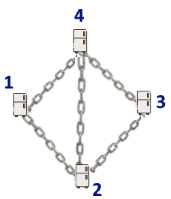 Например, на рисунке есть \(n=4\) людей и \(5\) цепей. Первый человек знает пароль для двух цепей: \(1-4\) и \(1-2\). \(1\)-й холодильник может открыть его владелец (\(1\)-й человек), а также \(2\)-й и \(4\)-й (работая сообща) могут его открыть.
Например, на рисунке есть \(n=4\) людей и \(5\) цепей. Первый человек знает пароль для двух цепей: \(1-4\) и \(1-2\). \(1\)-й холодильник может открыть его владелец (\(1\)-й человек), а также \(2\)-й и \(4\)-й (работая сообща) могут его открыть. Цены этих холодильников равны \(a_1, a_2, \ldots, a_n\). Чтобы сделать цепь, соединяющую холодильники \(u\) и \(v\), вы должны заплатить \(a_u + a_v\) долларов. Обратите внимание, что владелец квартиры позволяет вам сделать несколько цепей, соединяющих одну и ту же пару холодильников.
Хозяин квартиры, в которой живет Хань, просит вас создать ровно \(m\) цепей, чтобы все холодильники были защищены. Холодильник является защищенным тогда и только тогда, когда из \(n\) людей, живущих в квартире, только владелец холодильника может открыть его (то есть больше никто, действуя самостоятельно, не сможет его открыть). Другими словами, \(i\)-й холодильник не защищен, если существует человек \(j\) (\(i \ne j\)) такой, что \(j\) в одиночку сможет открыть \(i\)-й холодильник.
Например, на рисунке все холодильники защищены. С другой стороны, если есть \(n=2\) холодильника и только одна цепь (которая их соединяет), то оба холодильника не являются защищенными (оба холодильника могут быть открыты не только его владельцем, но и другим человеком).
Конечно, владелец хочет минимизировать общую стоимость всех цепей. Определите, существует ли какой-либо способ сделать ровно \(m\) цепей, и, если да, выведите любое решение, которое минимизирует суммарную стоимость.