Это упрощённая версия задачи. В этой версии \(n \le 2000\).
В трёхмерном пространстве заданы \(n\) различных точек, пронумерованных от \(1\) до \(n\). \(i\)-я точка имеет координаты \((x_i, y_i, z_i)\). Число точек \(n\) — чётное.
Вы хотели бы удалить все \(n\) точек, используя последовательность из \(\frac{n}{2}\) щелчков. За один щелчок вы можете удалить любые две ещё не удалённые точки \(a\) и \(b\), которые образуют идеально сбалансированную пару. Пара точек \(a\) и \(b\) идеально сбалансирована, если никакая другая точка \(c\) (которая ещё не удалена) не лежит в пределах минимального ограничивающего точки \(a\) и \(b\) прямоугольного параллелепипеда с рёбрами, параллельными осям координат.
Формально, точка \(c\) лежит внутри ограничивающего параллелепипеда точек \(a\) и \(b\) тогда и только тогда, когда \(\min(x_a, x_b) \le x_c \le \max(x_a, x_b)\), \(\min(y_a, y_b) \le y_c \le \max(y_a, y_b)\) и \(\min(z_a, z_b) \le z_c \le \max(z_a, z_b)\). Обратите внимание, что параллелепипед может быть вырожденным.
Найдите способ удалить все точки за \(\frac{n}{2}\) щелчков.
Выходные данные
Выведите \(\frac{n}{2}\) пар целых чисел \(a_i, b_i\) (\(1 \le a_i, b_i \le n\)) — номера точек, удаляемых щелчком \(i\). Каждое целое число от \(1\) до \(n\) должно встретиться в выводе ровно один раз.
Можно показать, что всегда возможно удалить все точки. Если есть несколько решений, выведите любое.
Примечание
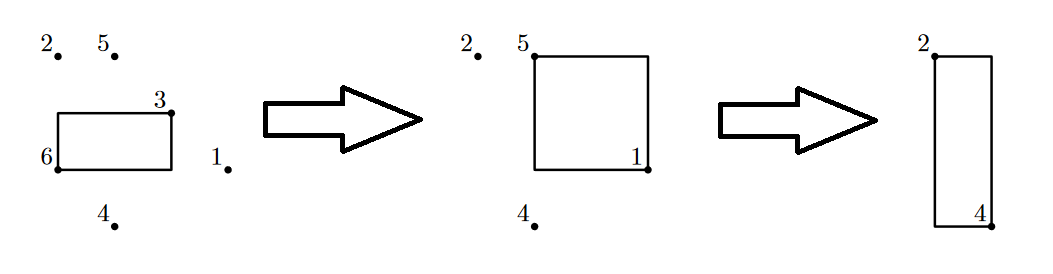
В первом примере точки и их соответствующие параллелепипеды выглядят так (изображённые для простоты в двумерном пространстве, так как все точки лежат на плоскости \(z = 0\)). Обратите внимание, что порядок удаления точек важен: например, точки \(5\) и \(1\) не образуют идеально сбалансированную пару изначально, но начинают её образовывать после того, как удалена точка \(3\).