Предположим, что есть прямоугольная таблица \(h \times w\), которая состоит из белых и черных ячеек. Определим следующее:
- \(r_{i}\) — Количество подряд идущих черных ячеек, с которых начинается \(i\)-я строка при просмотре слева направо (\(1 \le i \le h\)). В частности, \(r_i=0\), если крайняя левая ячейка \(i\)-й строки является белой.
- \(c_{j}\) — Количество подряд идущих черных ячеек, с которых начинается \(j\)-й столбец при просмотре сверху вниз (\(1 \le j \le w\)). В частности, \(c_j=0\), если самая верхняя ячейка \(j\)-го столбца является белой.
Иными словами, если \(i\)-я строка начинается ровно с \(r_i\) черных ячеек. Аналогично, \(j\)-й столбец начинается ровно с \(c_j\) черных ячеек.
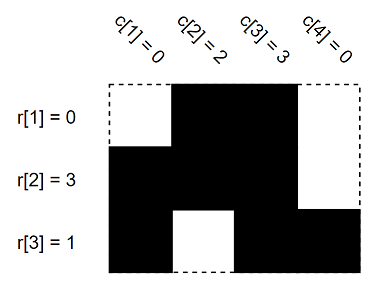Пример значений \(r\) и \(c\) таблицы \(3 \times 4\). Даны \(r\) и \(c\). Изначально все ячейки белые. Найдите количество способов заполнить ячейки так, чтобы в заданной таблице значения \(r\) и \(c\) были равны заданным. Поскольку ответ может быть очень большим, найдите по модулю \(1000000007\,(10^{9} + 7)\). Другими словами, найдите остаток от деления ответа на число \(1000000007\,(10^{9} + 7)\).
Выходные данные
Выведите ответ по модулю \(1000000007\,(10^{9} + 7)\).
Примечание
В первом примере есть другой возможный ответ.
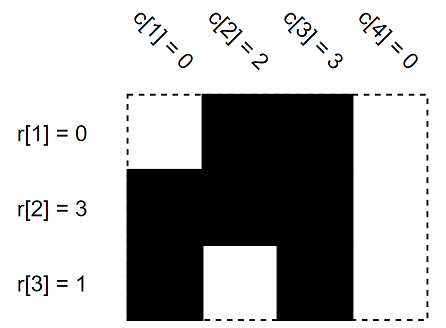
Во втором примере нет таких сеток, у которых \(r\) и \(c\) такие же.
В третьем примере убедитесь вывести ответ по модулю \((10^9 + 7)\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 4
0 3 1
0 2 3 0
|
2
|
|
2
|
1 1
0
1
|
0
|
|
3
|
19 16
16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12
6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4
|
797922655
|