В аэропортах часто используются траволаторы, потому что они помогают проходить большие расстояния быстрее. Каждый траволатор имеет некоторую собственную скорость, которая увеличивает скорость, с которой вы идёте. Вы можете просто стоять на траволаторе (тогда вы будете двигаться со скоростью траволатора), либо вы можете ещё и идти, тогда ваша итоговая скорость будет равна сумме скорости, с который вы идёте, и скорости траволатора.
Лимак хочет добраться из точки \(0\) в точку \(L\), расположенные на одной прямой. Между ними есть \(n\) дизъюнктных траволаторов. \(i\)-й из них описывается целыми числами \(x_i\), \(y_i\) и вещественным числом \(s_i\). \(i\)-й траволатор начинается в \(x_i\), заканчивается в \(y_i\) и имеет скорость \(s_i\).
Каждый траволатор расположен внутри отрезка \([0, L]\) и никакие два траволатора не имеют ненулевую длину пересечения. При этом траволаторы могут касаться.
Лимак хочет понять, как ему следует распределить свою энергию. Например, может быть оптимально стоять где-нибудь (или идти с низкой скоростью), чтобы сэкономить энергию и потом идти быстрее.
Изначально энергия Лимака равна \(0\), и она никогда не должна падать ниже этого значения. В каждый момент он может идти со скоростью \(v\) в диапазоне \([0, 2]\), и это будет стоить ему \(v\) энергии. Также его энергия постоянно пополняется со скоростью \(1\) единица энергии в секунду. Таким образом, если он идёт со скоростью \(v\), его энергия растёт со скоростью \((1-v)\). Обратите внимание, что негативный рост означает убывание энергии.
В частности, Лимак может идти со скоростью \(1\), и это никак не будет влиять на его уровень энергии, а если он будет идти со скорость \(0.77\), то энергия будет расти на \(0.23\).
Лимак может выбирать свою скорость произвольным образом (любое вещественное число в диапазоне \([0, 2]\)) в каждый момент времени (в том числе в моменты, когда он находится в нецелых позициях). Всё происходит непрерывно (не дискретно).
За какое минимальное время Лимак сможет добраться из \(0\) в \(L\)?
Примечание
Картинка изображает первые два примера. В первом примере есть траволатор из \(0\) в \(2\) скорости \(2.0\), а Лимак хочет попасть в точку \(5\). Во втором примере есть траволатор из \(2\) в \(4\) скорости \(0.91\).
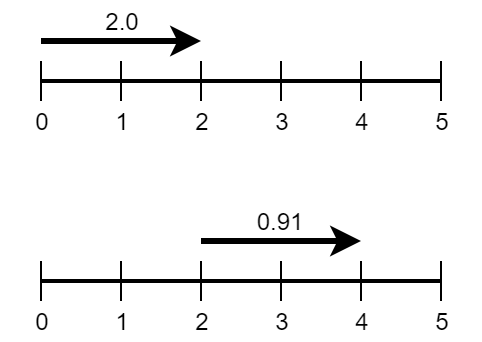
В первом примере, одна из оптимальных стратегий выглядит следующим образом.
- Добраться из \(0\) в \(2\) просто стоя на траволаторе. Траволатор едет со скоростью \(2\), значит понадобится всего \(1\) секунда времени и энергия увеличится на \(1\).
- Добраться из \(2\) в \(4\) идя со скоростью \(2\) в течении \(1\) секунды. За эту \(1\) секунду уровень энергии понизится до \(0\).
- Добраться из \(4\) в \(5\) идя со скоростью \(1\). На это понадобится \(1\) секунда и уровень энергии будет равен \(0\) всё это время.
Тем самым общее время равно \(1 + 1 + 1 = 3\).