Это интерактивная задача
Дано клетчатое поле \(n\times n\), где \(n\) нечетное. Строки пронумерованы от \(1\) до \(n\) сверху вниз, столбцы пронумерованы от \(1\) до \(n\) слева вправо. Клетка, стоящая на пересечении \(x\)-й строки и \(y\)-го столбца, будет обозначаться как \((x, y)\).
В каждой клетке записан \(0\) или \(1\). Известно, что в верхней левой клетке записана \(1\), а в нижней правой записан \(0\).
Мы хотим узнать, что записано в каждой клетке поля. Для этого мы можем задавать вопросы вида:
«\(?\) \(x_1\) \(y_1\) \(x_2\) \(y_2\)», где \(1 \le x_1 \le x_2 \le n\), \(1 \le y_1 \le y_2 \le n\), и \(x_1 + y_1 + 2 \le x_2 + y_2\). Другими словами, мы выводим две различные клетки \((x_1, y_1)\), \((x_2, y_2)\) поля такие, что из первой можно добраться во вторую, идя только вправо и вниз, причем они не являются соседними.
В ответ на такой запрос вы узнаете, существует ли путь между \((x_1, y_1)\) и \((x_2, y_2)\), идущий по клеткам только вправо или вниз, числа в клетках которого образуют палиндром.
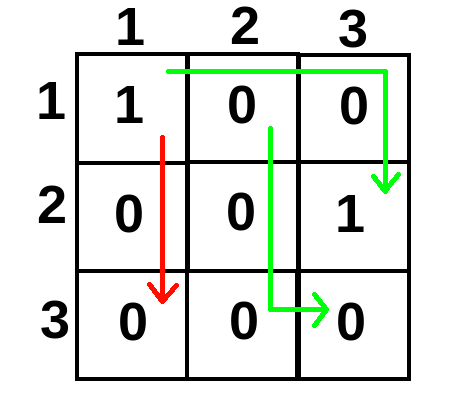
К примеру, пути, изображенные зеленым, являются палиндромными, поэтому ответ для «\(?\) \(1\) \(1\) \(2\) \(3\)» и «\(?\) \(1\) \(2\) \(3\) \(3\)» был бы, что такой путь существует. В то же время между точками \((1, 1)\) и \((3, 1)\) не существует палиндромного пути.
Определите все клетки поля, задав не более \(n^2\) вопросов. Можно показать, что ответ всегда существует.
Протокол взаимодействия
Вы начинаете взаимодействие, считав \(n\).
Чтобы задать вопрос о клетках \((x_1, y_1), (x_2, y_2)\), в одной строке выведите «\(?\) \(x_1\) \(y_1\) \(x_2\) \(y_2\)».
Числа в запросе должны удовлетворять условиям \(1 \le x_1 \le x_2 \le n\), \(1 \le y_1 \le y_2 \le n\), и \(x_1 + y_1 + 2 \le x_2 + y_2\). Не забудьте сделать операцию 'flush', чтобы получить ответ.
В ответ на заданный вопрос вы получите \(1\), если существует путь идущий с \((x_1, y_1)\) в \((x_2, y_2)\) только вправо или вниз, числа в клетках которого образуют палиндром, и \(0\) в противном случае.
В случае, если ваш запрос не соответствует требованиям, или вы задали более \(n^2\) запросов, программа выведет \(-1\) и прекратит взаимодействие. Вы получите вердикт Неправильный ответ. Вам нужно завершить работу вашей программы, чтобы не получить другие вердикты.
Когда вы установите все числа в клетках, выведите «!».
Далее выведите \(n\) строк, \(i\)-я из которых — строка длины \(n\), соответствующая числам в строке \(i\) поля.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат для взломов
Чтобы взламывать, используйте следующий формат.
Первая строка должна содержать единственное нечетное число \(n\) (сторона вашего поля).
\(i\)-я из \(n\) последующих строчек должна содержать строку длины \(n\) соответствующую \(i\)-й строке поля. Верхний левый элемент должен равняться \(1\), нижний правый \(0\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
0
1
0
1
1
1
1
|
? 1 1 1 3
? 1 1 2 3
? 2 1 2 3
? 3 1 3 3
? 2 2 3 3
? 1 2 3 2
? 1 2 3 3
!
100
001
000
|