Дано целое положительное число \(n\). Нужно расставить числа от \(1\) до \(2n\) по кругу таким образом, чтобы выполнялось следующее условие:
Для каждых \(n\) последовательных чисел на окружности выпишем на доску их сумму. Тогда любые два из выписанных на доске \(2n\) чисел отличаются не более, чем на \(1\).
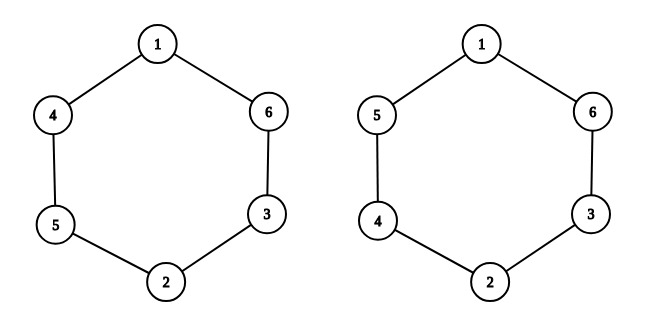
К примеру, выберем \(n = 3\). Слева вы можете увидеть пример правильной расстановки:\(1 + 4 + 5 = 10\), \(4 + 5 + 2 = 11\), \(5 + 2 + 3 = 10\), \(2 + 3 + 6 = 11\), \(3 + 6 + 1 = 10\), \(6 + 1 + 4 = 11\), любые два числа отличаются не более чем на \(1\). Справа вы можете увидеть неправильную расстановку: к примеру, \(5 + 1 + 6 = 12\), а \(3 + 2 + 4 = 9\), \(9\) и \(12\) отличаются более чем на \(1\).
Выходные данные
Если решения не существует, в первой строке выведите «NO».
Если оно существует, в первой строке выведите «YES». После чего, во второй строке выведите \(2n\) чисел — числа от \(1\) до \(2n\) в порядке в котором они будут стоять на окружности. Каждое число должно встречаться только один раз. Если есть несколько решений, выведите любое.
Примечание
Пример из условия приведен для первого примера.
Можно доказать, что для второго примера решения не существует.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
|
YES
1 4 5 2 3 6
|
|
2
|
4
|
NO
|