Олимпиадный тренинг

Задача . E. Раздвижные двери

Задача

Представьте, вы — директор крупной традиционной компании. И, в отличие от современных передовых компаний (таких как JetBrains), в вашей введен дресс-код. Поэтому вы уже подготовили под раздевалку для сотрудников просторную комнату. Более того, вы успели приобрести $m$-секционный шкаф, в котором ваши сотрудники будут хранить свои вещи. А точнее, $i$-й сотрудник хранит свои принадлежности в $i$-й секции (разумеется, все секции имеют равные размеры).

Однако возникла проблема: у шкафа раздвижные двери! А именно, в шкаф встроенно $n$ дверей (пронумерованных слева направо) и $j$-я дверь имеет ширину, равную $a_j$ секций шкафа. Но при этом, все двери установлены на одних направляющих.

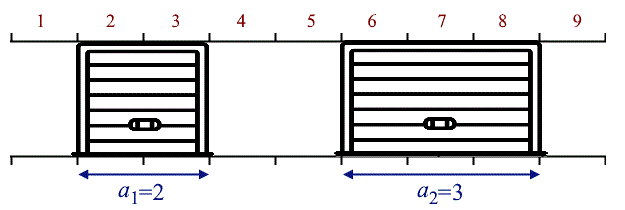$\text{[math]}$ Крайне схематичный пример шкафа: $m=9$, $n=2$, $a_1=2$, $a_2=3$.

Проблема же в следующем: иногда, чтобы открыть некоторые секции приходится перекрывать другие (так как двери ходят по одним направляющим). Например, представим $4$-секционный шкаф (т.е. $m=4$) с $n=2$ одинарными дверями (т.е. $a_1=a_2=1$) и вам надо открыть $1$-ю и $3$-ю секции — вам придется перекрыть $2$-ю и $4$-ю секции.

Будучи директором, вы имеете на руках полное расписание на следующие $q$ дней. И теперь вас интересует следующий вопрос: смогут ли все сотрудники, кто придет в $k$-й день, открыть свои секции одновременно.

Входные данные

В первой строке заданы два целых числа $n$ и $m$ ($1 \le n \le 2 \cdot 10^5$, $1 \le m \le 4 \cdot 10^5$) — количество дверей и секций соответственно.

Во второй строке заданы $n$ целых чисел $a_1, a_2, \dots, a_n$ ($1 \le a_i \le m$, $\sum{a_i} \le m$) — соответствующая ширина дверей.

В третьей строке задано единственное целое число $q$ ($1 \le q \le 2 \cdot 10^5$) — количество дней, которые вам необходимо обработать.

В следующих $q$ строках заданы расписания каждого дня. Каждое расписание представляет из себя целое число $c_k$ и следующие за ним $c_k$ целых чисел $w_1, w_2, \dots, w_{c_k}$ ($1 \le c_k \le 2 \cdot 10^5$, $1 \le w_1 < w_2 < \dots < w_{c_k} \le m$) — количество сотрудников, которые придут в $k$-й день, и их номера в возрастающем порядке.

Гарантируется, что $\sum{c_k}$ не превосходит $2 \cdot 10^5$.

Выходные данные

Выведите $q$ ответов. Каждый ответ — это «YES» или «NO» (без учета регистра). Выведите «YES» если все сотрудники, которые придут в текущий день, смогут открыть свои секции одновременно.

Примеры

№	Входные данные	Выходные данные
1	3 10 2 3 2 6 1 5 2 1 10 2 2 9 2 5 6 3 1 7 8 4 1 2 3 4	YES YES NO NO YES NO

time 3000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет