В одной волшебной стране ровно \(n\) городов, пронумерованных \(1, 2, \dots, n\). Некоторые пары городов соединены волшебными цветными дорогами. Волшебство непостоянно, поэтому иногда между городами возникают новые дороги.
Работа ведьмы Вики — доставлять посылки из одних городов в другие. Вики — новичок, поэтому она может выполнить доставку, только если существует двойной радужный путь из начального города в конечный. Двойным радужным путем называется последовательность городов \(c_1, c_2, \dots, c_k\), удовлетворяющая следующим свойствам:
- Для каждого \(i\), где \(1 \le i \le k - 1\), города \(c_i\) и \(c_{i + 1}\) соединены дорогой.
- Для каждого \(i\), где \(1 \le i \le \frac{k - 1}{2}\), дороги, соединяющие \(c_{2i}\) с городами \(c_{2i - 1}\) и \(c_{2i + 1}\), должны иметь один и тот же цвет.
Например, если \(k = 5\), то дорога между городами \(c_1\) и \(c_2\) должна быть того же цвета, что и дорога между \(c_2\) и \(c_3\), а дорога между \(c_3\) и \(c_4\) должна иметь тот же цвет, что и дорога между \(c_4\) и \(c_5\).
У Вики есть список событий в хронологическом порядке. Каждое событие — это либо доставка, которую она должна выполнить, либо появление новой дороги. Помогите ей определить, какие доставки она сможет выполнить.
Выходные данные
Для каждого события сторого типа выведите одну строку, содержащую «Yes» (без кавычек), если доставку можно осуществить, и «No» (без кавычек) иначе.
Примечание
Пример соответствует рисунку.
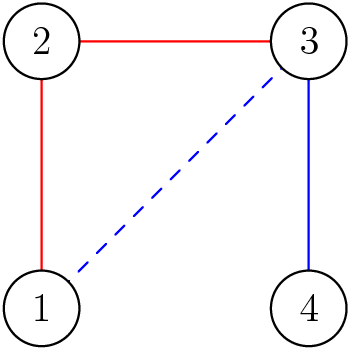
Для первой доставки Вики может использовать путь 1, 2, 3, 4, который является двойным радужным. Вторую доставку нельзя осуществить, так как лучшее, что может сделать Вики — добраться до города \(3\). После добавления новой дороги между городами \(1\) и \(3\), Вики может добраться из города \(4\) в город \(1\) по двойному радужному пути 4, 3, 1.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 3 2 4
1 2 1
2 3 1
3 4 2
? 1 4
? 4 1
+ 3 1 2
? 4 1
|
Yes
No
Yes
|