К счастью Сервалу повезло попасть на нужный автобус, и он успел приехать в детский сад вовремя. В детском саду ему сразу же понравились игрушечные кубики.
У него есть интересное хобби — придумывать разные задачки и давать их решать другим. В этот раз с помощью кубиков \(1 \times 1 \times 1\) он построил трехмерную фигуру. Эту фигуру можно описать матрицей \(n \times m\), что на клетке \((i,j)\) стоят друг на друге \(h_{i,j}\) кубиков.
Сервал не расскажет вам \(h_{i,j}\), он даст вам только вид спереди, вид слева, и вид сверху этой фигуры, и попросит вас восстановить фигуру. Вид спереди описывается \(m\) столбцами, и высота \(i\)-го из них равна максимуму среди \(h_{1,i},h_{2,i},\dots,h_{n,i}\). Аналогично описывается и вид слева, он задан \(n\) столбцами. Вид сверху описывается матрицей \(n \times m\) \(t_{i,j}\), где \(t_{i,j}\) равно \(0\) или \(1\). \(t_{i,j}\), равное \(1\), означает, что \(h_{i,j}>0\), иначе \(h_{i,j}=0\).
К сожалению, Сервалу очень одиноко, потому что все устали от его прошлых неразрешимых задач. Они отказываются решать эту даже несмотря на то, что в этот раз он обещает, что найдется хотя бы одна фигура, подходящая под все данные виды. Как его лучший друг, может быть, вы ее решите?
Выходные данные
Выведите \(n\) строк, по \(m\) целых чисел в каждой, \(j\)-е число в \(i\)-й строке должно быть равно высоте фигуры в соотвествующей позиции. Если существует несколько подходящих фигур, вы можете вывести любую.
Примечание
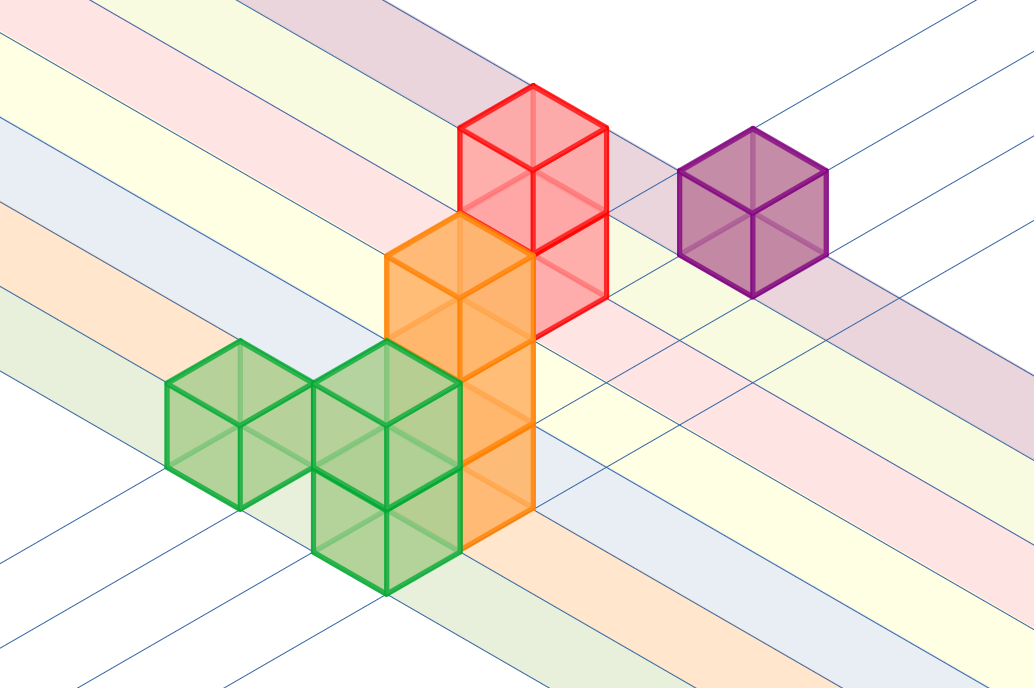
На приведенной выше иллюстрации изображена фигура из первого примера.
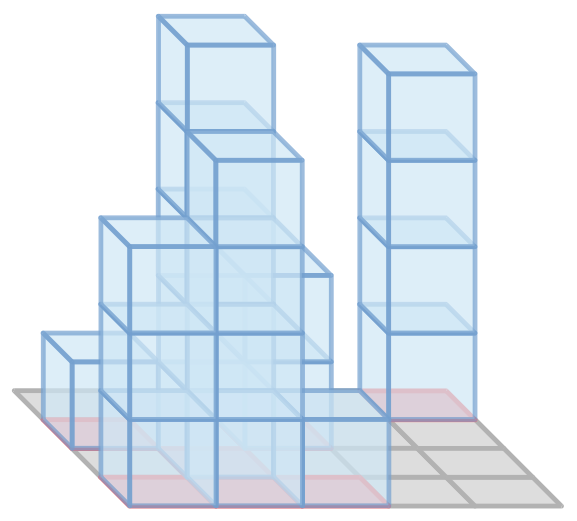
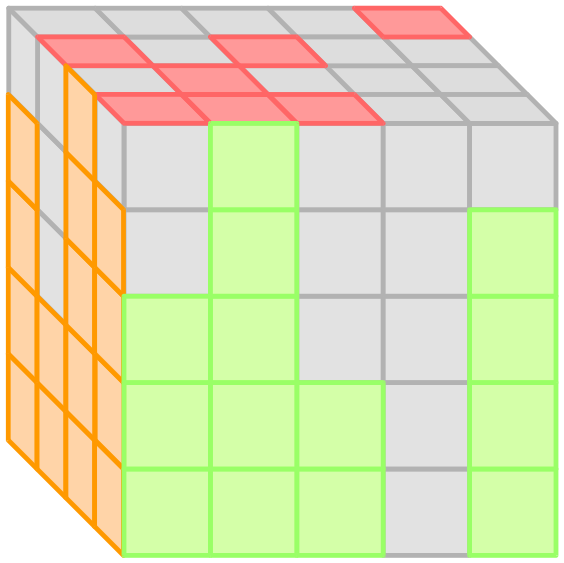
На первой из двух этих иллюстраций изображена фигура из второго примера, а на второй изображены три ее вида.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 7 3
2 3 0 0 2 0 1
2 1 3
1 0 0 0 1 0 0
0 0 0 0 0 0 1
1 1 0 0 0 0 0
|
1 0 0 0 2 0 0
0 0 0 0 0 0 1
2 3 0 0 0 0 0
|
|
2
|
4 5 5
3 5 2 0 4
4 2 5 4
0 0 0 0 1
1 0 1 0 0
0 1 0 0 0
1 1 1 0 0
|
0 0 0 0 4
1 0 2 0 0
0 5 0 0 0
3 4 1 0 0
|