Задан неориентированный невзвешенный связный граф, состоящий из \(n\) вершин и \(m\) ребер. Гарантируется, что в графе отсутствуют петли и кратные ребра.
Ваша задача — найти любое такое покрывающее дерево этого графа, что степень первой вершины (вершины с номером \(1\)) вершины равна \(D\) (или сказать, что таких покрывающих деревьев не существует). Напомним, что степень вершины — это количество ребер, инцидентных ей.
Выходные данные
Если не существует покрывающего дерева, удовлетворяющего условию задачи выведите «NO» в первой строке.
Иначе выведите «YES» в первой строке и затем выведите \(n-1\) строк, описывающих ребра такого покрывающего дерева, что степень первой вершины (вершины с номером \(1\)) равна \(D\). Убедитесь, что ребра выводимого покрывающего дерева представляют собой подмножество ребер входных данных (порядок ребер не важен, также ребро \((v, u)\) может быть выведено как \((u, v)\)).
Если существует несколько возможных ответов, выведите любой.
Примечание
Картинка, соответствующая первому и второму тестовым примерам: 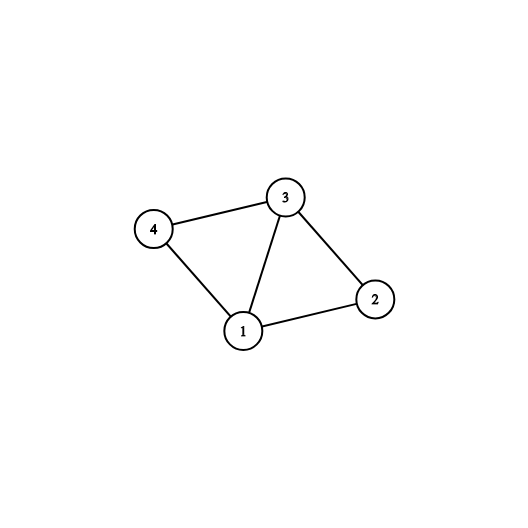
Картинка, соответствующая третьему тестовому примеру: 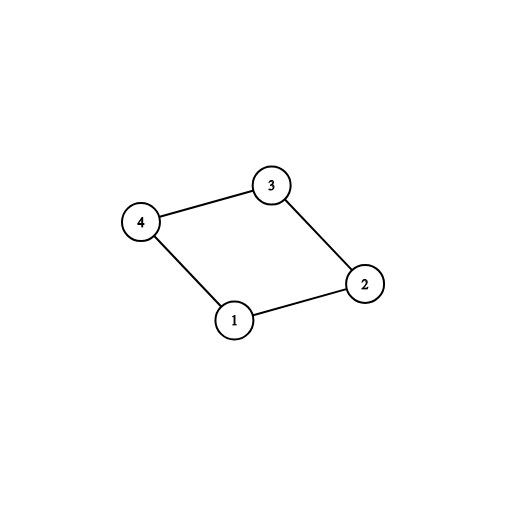
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 5 1
1 2
1 3
1 4
2 3
3 4
|
YES
2 1
2 3
3 4
|
|
2
|
4 5 3
1 2
1 3
1 4
2 3
3 4
|
YES
1 2
1 3
4 1
|
|
3
|
4 4 3
1 2
1 4
2 3
3 4
|
NO
|