Боб подарил Алисе набор Toy Train™ (игрушечный поезд). Он состоит из одного поезда и связной железной дороги из \(n\) станций, пронумерованных от \(1\) до \(n\). Поезд занимает одну станцию в один момент времени и перемещается по железнодорожной сети станций по кругу. Более точно, поезд посетит станцию \(i+1\) сразу после станции \(i\), если \(1 \leq i < n\), или станцию \(1\), если \(i = n\). Поезду требуется \(1\) секунда, чтобы по описанному процессу переместиться на следующую станцию.
Боб оставил Алисе интересную задачку перед уходом: доставить \(m\) конфет, которые исходно находятся на некоторых станциях, на их независимые места назначения с помощью поезда. Конфеты пронумерованы от \(1\) до \(m\). Конфета \(i\) (\(1 \leq i \leq m\)), сейчас находящаяся на станции \(a_i\), должна быть доставлена на станцию \(b_i\) (\(a_i \neq b_i\)).
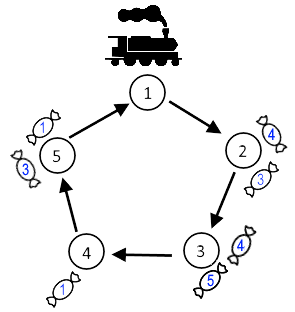Синие числа на конфетах соответствуют значениям \(b_i\). Картинка соответствует примеру \(1\). У поезда бесконечная вместимость, на станции можно выгружать неограниченное количество конфет. Но не более одной конфеты может быть загружено со станции на поезд до того, как он ее покинет. Вы можете выбрать любую из конфет на этой станции. Временем, которое требуется поезду, чтобы загрузить на него конфету, можно пренебречь.
Алиса хочет узнать, за какое минимальное время поезд может доставить все конфеты. Ваша задача — узнать для каждой станции, за какое минимальное время поезд сможет доставить все конфеты, если он начнет с этой станции.
Выходные данные
В первой и единственной строке вывода выведите \(n\) целых чисел, разделенных пробелами, \(i\)-е из них это минимальное время, в секундах, которое нужно поезду, чтобы доставить все конфеты, начав со станции \(i\).
Примечание
Рассмотрим второй тестовый пример.
Если поезд начнет со станции \(1\), будет следующая оптимальная стратегия:
- Загрузить первую конфету в поезд.
- Добраться до станции \(2\). Это займет \(1\) секунду.
- Доставить первую конфету.
- Добраться до станции \(1\). Это займет \(1\) секунду.
- Загрузить вторую конфету в поезд.
- Добраться до станции \(2\). Это займет \(1\) секунду.
- Доставить вторую конфету.
- Добраться до станции \(1\). Это займет \(1\) секунду.
- Загрузить третью конфету в поезд.
- Добраться до станции \(2\). Это займет \(1\) секунду.
- Доставить третью конфету.
Таким образом, поезду требуется \(5\) секунд чтобы завершить задания.
Если поезд стартует на станции \(2\), ему нужно будет добраться до станции \(1\) перед загрузкой первой конфеты, на что потребуется еще одна секунда. Таким образом, ответ в этом случае будет \(5+1 = 6\) секунд.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5 7
2 4
5 1
2 3
3 4
4 1
5 3
3 5
|
10 9 10 10 9
|
|
2
|
2 3
1 2
1 2
1 2
|
5 6
|