Назовем некоторую квадратную матрицу с целыми числами в ячейках палиндромной, если она не меняется при изменении порядка строк на обратный и не меняется при изменении порядка столбцов на обратный.
Например, следующие матрицы палиндромные:
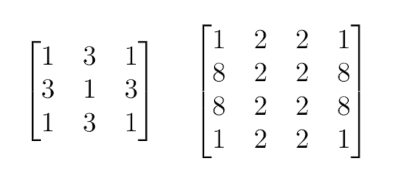
Следующие матрицы не палиндромные, потому что меняются при изменении порядка строк на обратный:
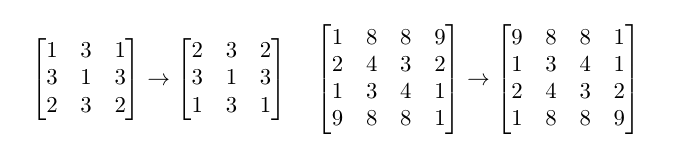
Следующие матрицы не палиндромные, потому что меняются при изменении порядка столбцов на обратный:
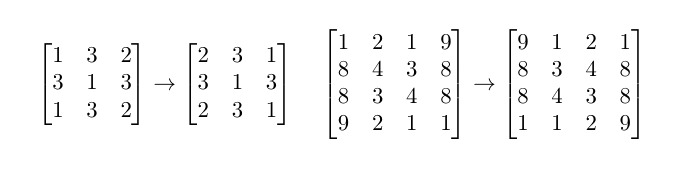
Заданы \(n^2\) целых чисел. Разместите их в матрице из \(n\) строк и \(n\) столбцов так, чтобы каждое число было использовано ровно один раз, каждая ячейка содержала ровно одно число и полученная матрица была палиндромной. Если существует несколько решений, выведите любое из них. Если решения не существует, выведите «NO».
Выходные данные
Если можно разместить все \(n^2\) чисел в матрице из \(n\) строк и \(n\) столбцов так, чтобы каждое число было использовано ровно один раз, каждая ячейка содержала ровно одно число и полученная матрица была палиндромной, то выведите «YES». Затем выведите \(n\) строк, каждая должна содержать \(n\) целых чисел, разделенных пробелами, — полученная матрица.
Если невозможно собрать ни одну матрицу, то выведите «NO».
Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, «YeS», «no» и «yES» принимаются.
Примечание
Обратите внимание, что существует несколько возможных ответов для первых двух примеров.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
1 8 8 1 2 2 2 2 2 2 2 2 1 8 8 1
|
YES
1 2 2 1
8 2 2 8
8 2 2 8
1 2 2 1
|
|
2
|
3
1 1 1 1 1 3 3 3 3
|
YES
1 3 1
3 1 3
1 3 1
|
|
3
|
4
1 2 1 9 8 4 3 8 8 3 4 8 9 2 1 1
|
NO
|
|
4
|
1
10
|
YES
10
|