В кругу сидят \(n\) человек, которые пронумерованы от \(1\) до \(n\) в том порядке, в котором они сидят. То есть для каждого \(i\) от \(1\) до \(n-1\) люди с номерами \(i\) и \(i+1\) являются соседями. Кроме того, люди с номерами \(n\) и \(1\) также являются соседями.
У человека с номером \(1\) изначально есть мяч. Он выбирает положительное целое число \(k\) не больше \(n\) и кидает мяч своему \(k\)-му соседу в сторону увеличения номеров, этот человек также кидает мяч своему \(k\)-му соседу в ту же сторону и так далее, пока человек с номером \(1\) не получит мяч обратно. Когда он получит его обратно, люди больше не кидают мяч.
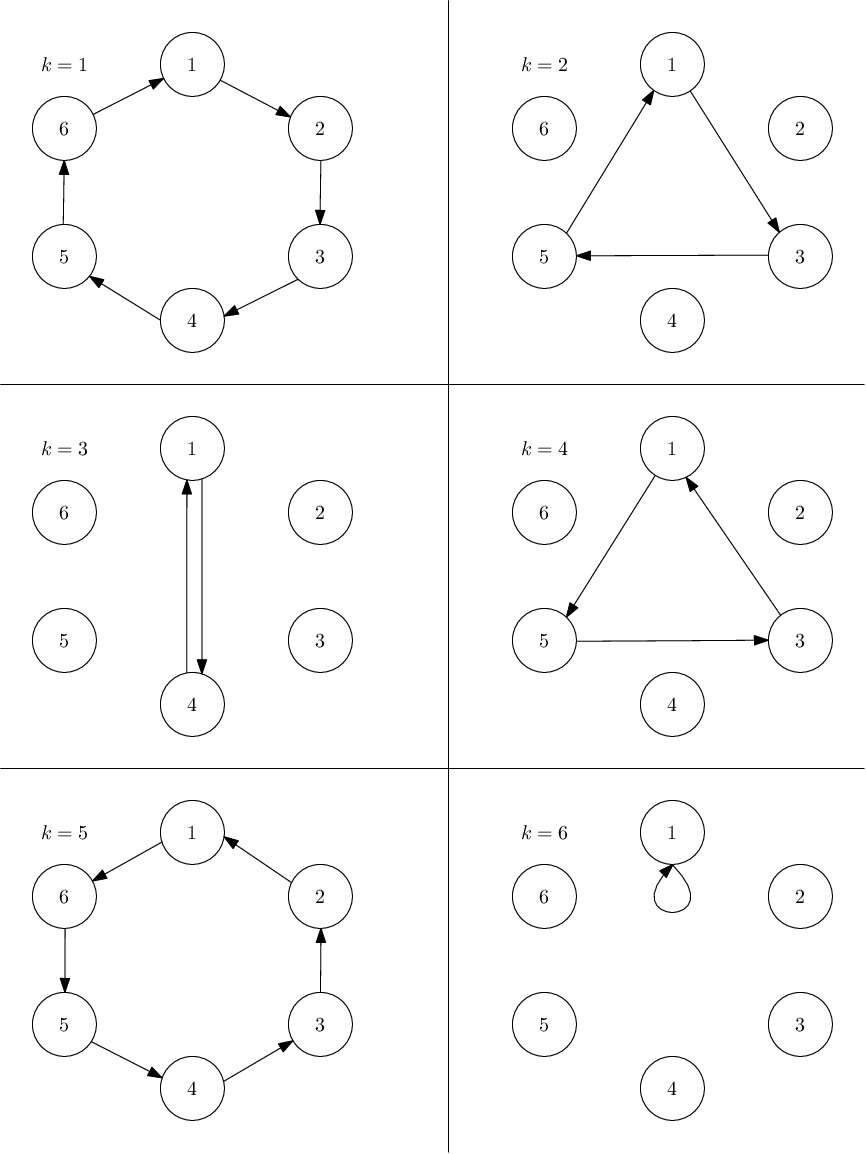
Например, если \(n = 6\) и \(k = 4\), то мяч пройдет по игрокам с номерами \([1, 5, 3, 1]\).
Рассмотрим набор всех людей, у которых был мяч. Уровень веселья игры — это сумма номеров всех людей, у которых был мяч. В приведенном выше примере уровень веселья будет \(1 + 5 + 3 = 9\).
Найдите набор возможных уровней веселья для всех вариантов положительного целого числа \(k\). Можно показать, что при ограничениях задачи мяч всегда возвращается к \(1\)-му игроку после конечного числа бросков, и для заданного \(n\) существует не более \(10^5\) возможных уровней веселья.
Выходные данные
Предположим, что множество уровней веселья — \(f_1, f_2, \dots, f_m\).
Выведите в одной строке \(m\) целых чисел, разделенных пробелом, от \(f_1\) до \(f_m\) в возрастающем порядке.
Примечание
В первом примере мы уже показали, что выбор \(k = 4\) дает уровень веселья \(9\), так же как и \(k = 2\). Если выбрать \(k = 6\), то уровень веселья будет \(1\). Для \(k = 3\) мы получаем уровень веселья \(5\), а с \(k = 1\) или \(k = 5\) мы получаем \(21\).
Во втором примере значения \(1\), \(10\), \(28\), \(64\) и \(136\) можно получить, например, при \(k = 16\), \(8\), \(4\), \(10\) и \(11\), соответственно.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
|
1 5 9 21
|
|
2
|
16
|
1 10 28 64 136
|