Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются.
Однажды Пете попался отрезок чисел [a, a + l - 1]. Пусть F(x) — количество счастливых цифр числа x. Найдите минимальное b (a < b) такое, что F(a) = F(b), F(a + 1) = F(b + 1), ..., F(a + l - 1) = F(b + l - 1).
Выходные данные
В единственной строке выведите число b — ответ на задачу.
Примечание
Считайте, что [a, b] обозначает отрезок целых чисел, включающий границы. То есть 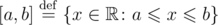
Примеры
| № | Входные данные | Выходные данные |
|
1
|
7 4
|
17
|
|
2
|
4 7
|
14
|