Поскольку Соня недавно выучила основы матриц, она решила немножко поиграть с ними.
Соня быстро придумала новый вид матриц, которые назвала ромбические матрицы. Эти матрицы имеют ровно один ноль, а во всех остальных ячейках записано манхэттенское расстояние до клетки с нулём. Ячейки с одинаковыми числами имеют форму ромбов, поэтому, Соня так этот вид и назвала.
Манхэттенское расстояние между ячейками (\(x_1\), \(y_1\)) и (\(x_2\), \(y_2\)) равно величине \(|x_1 - x_2| + |y_1 - y_2|\). Например, манхэттенское расстояние между ячейками \((5, 2)\) и \((7, 1)\) равно \(|5-7|+|2-1|=3\).
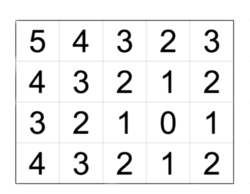 Пример ромбической матрицы.
Пример ромбической матрицы. Отметим, что ромбическая матрица однозначно задается своими размерами \(n\), \(m\) и положением ячейки со значением \(0\).
Она нарисовала некоторую \(n\times m\) ромбическую матрицу. Девочка полагает, что вы не сможете возобновить матрицу, если она вам даст только элементы матрицы в случайном порядке (то есть последовательность из \(n\cdot m\) чисел). Отметим, что Соня не даст вам сами числа \(n\) и \(m\), в вашем распоряжении будет только последовательность всех элементов матрицы.
Напишите программу, которая найдет такую \(n\times m\) ромбическую матрицу, что её элементы — это в точности все элементы заданной последовательности, расположенные в матрице подходящим образом.
Выходные данные
В первой строке выведите два целых положительных числа \(n\) и \(m\) (\(n \times m = t\)) — размеры матрицы.
В следующей строке выведите два целых числа \(x\) и \(y\) (\(1\leq x\leq n\), \(1\leq y\leq m\)) — номер строки и номер колонки, на пересечении которых расположена ячейка со значением \(0\).
Если существует несколько решений, выведите любое из них. Если решения не существует, выведите одно целое число \(-1\).
Примечание
Рисунок к первому примеру можно увидеть в легенде. Так же можно выбрать ячейку \((2, 2)\) для нуля. Кроме этого, матрица \(5\times 4\) с нулём в \((4, 2)\) тоже является правильной.
Для второго примера существует матрица размером \(3\times 6\), ноль которой находится в ячейки \((2, 3)\).
Для третьего примера решения не существует.