Задано \(n\) отрезков на координатной прямой; концы отрезков имеют целочисленные координаты. Отрезки могут вырождаться в точки. Отрезки могут пересекаться друг с другом, вкладываться и даже совпадать.
Ваша задача: для каждого \(k \in [1..n]\) посчитать количество таких точек с целочисленными координатами, что количество отрезков, покрывающих эти точки, равно \(k\). Отрезок с границами \(l_i\) и \(r_i\) покрывает точку \(x\) тогда и только тогда, когда \(l_i \le x \le r_i\).
Выходные данные
Выведите \(n\) целых чисел через пробел \(cnt_1, cnt_2, \dots, cnt_n\), где \(cnt_i\) равно количеству таких точек, что количество отрезков, покрывающих эти точки, равно \(i\).
Примечание
Картинка, описывающая первый тестовый пример:
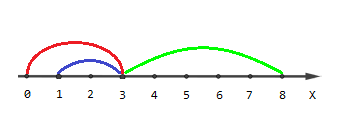
Точки с координатами \([0, 4, 5, 6, 7, 8]\) покрыты одним отрезком, точки \([1, 2]\) покрыты двумя отрезками и точка \([3]\) покрыта тремя отрезками.
Картинка, описывающая второй тестовый пример:
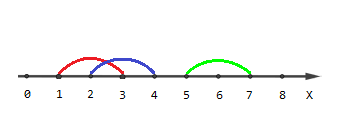
Точки \([1, 4, 5, 6, 7]\) покрыты одним отрезком, точки \([2, 3]\) покрыты двумя отрезками и точек, покрытых тремя отрезками, нет.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
0 3
1 3
3 8
|
6 2 1
|
|
2
|
3
1 3
2 4
5 7
|
5 2 0
|