Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям.
Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть антицентром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера максимальна. Для каждого кластера гарантируется единственность его антицентра. Расстояние между двумя точками А (х1, y1) и B (х2, y2) на плоскости вычисляется по формуле:
\(𝑑(𝐴,𝐵)=\sqrt{(𝑥2-𝑥1)^2+(𝑦2-𝑦1)^2}\)
В файле А хранятся координаты точек двух кластеров, где Н=8, W=4 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата х, затем координата у. Значения даны в условных единицах. Известно, что количество точек не превышает 1000.
В файле Б хранятся координаты точек трёх кластеров, где Н=6, W=7 для каждого кластера. Известно, что количество точек не превышает 10 000. Структура хранения информации о звёздах в файле Б аналогична структуре в файле А.
Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, представляющих аномалии, которые возникли в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла А определите координаты антицентра каждого кластера, затем вычислите два числа: P1 – сумма абсциссы и ординаты антицентра кластера с наименьшим количеством точек, и P2 – сумма абсциссы и ординаты антицентра кластера с наибольшим количеством точек. Гарантируется, что во всех кластерах количество точек различно.
Для файла Б определите координаты антицентра каждого кластера, затем вычислите два числа: Qx – абсциссу наиболее отдалённого антицентра кластера от начала координат, и Qy – ординату ближайшего антицентра кластера к началу координат.
В ответе запишите четыре числа: в первой строке – сначала целую часть абсолютного значения произведения P1 × 10 000, затем целую часть абсолютного значения произведения P2 × 10 000; во второй строке – сначала целую часть абсолютного значения произведения Qx × 10 000, затем целую часть абсолютного значения произведения Qy × 10 000.
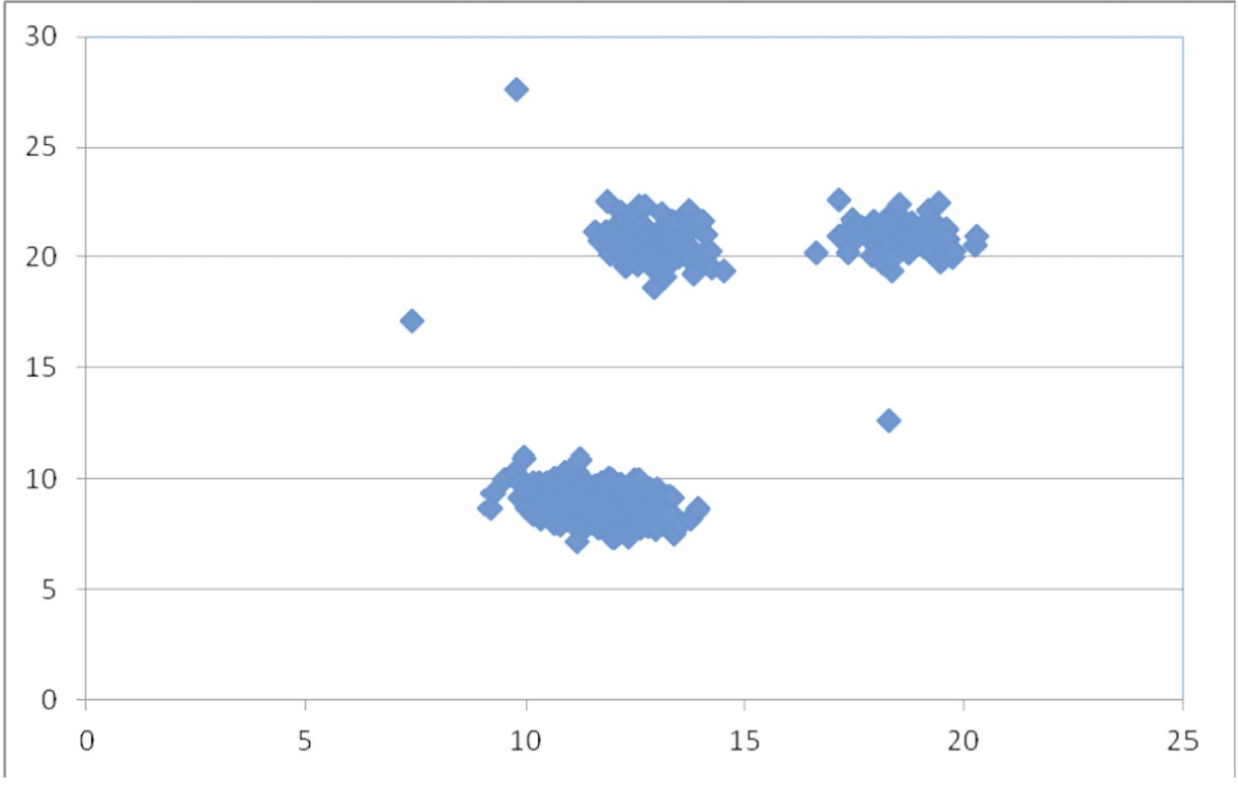
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.