Проблема полного перебора
В предыдущей задаче мы нашли лучшие w и b методом полного перебора. Но у этого подхода есть серьёзные проблемы:
- Для 1 признака мы перебрали ~1600 вариантов
- Для 10 признаков пришлось бы перебрать миллиарды вариантов
- Для 100 признаков (обычный датасет) — это вообще невозможно
Нужен умный способ, который не перебирает всё подряд, а движется в правильном направлении.
Аналогия: спуск с горы в тумане
 Представьте: вы стоите на склоне горы в густом тумане и хотите спуститься вниз. Вы не видите всю гору целиком, только то, что под ногами.
Представьте: вы стоите на склоне горы в густом тумане и хотите спуститься вниз. Вы не видите всю гору целиком, только то, что под ногами.
Что вы делаете?
- Смотрите, куда склон идёт вниз
- Делаете шаг в этом направлении
- Снова смотрите, куда склон идёт вниз
- Повторяете, пока не окажетесь на дне
Это и есть градиентный спуск!
Градиентный спуск: основная идея
У нас есть функция ошибки (log-loss), которая зависит от w и b. Можно представить её как поверхность:
- На оси X — значения \( w \)
- На оси Y — значения \( b \)
- Высота — величина ошибки
Цель: найти самую низкую точку этой поверхности (минимум ошибки).
Алгоритм:
- Начинаем со случайных значений \( w \) и \( b \) (или с нулей)
- Смотрим, в какую сторону нужно их изменить, чтобы ошибка уменьшилась
- Делаем маленький шаг в этом направлении
- Повторяем много раз
Что такое градиент (без сложной математики)?
Градиент — это просто стрелка, которая показывает направление самого быстрого роста функции.
Если функция ошибки растёт в направлении стрелки, значит в обратном направлении она падает!
Для наших параметров градиент показывает:
- Нужно ли увеличить или уменьшить \( w \)
- Нужно ли увеличить или уменьшить \( b \)
- Насколько сильно изменить каждый параметр
Формулы обновления (интуитивно)
На каждом шаге мы обновляем параметры по правилу:
\[ w_{\text{новое}} = w_{\text{старое}} - \alpha \cdot \frac{\partial \text{Loss}}{\partial w} \]
\[ b_{\text{новое}} = b_{\text{старое}} - \alpha \cdot \frac{\partial \text{Loss}}{\partial b} \]
Что означают эти символы?
- \( \frac{\partial \text{Loss}}{\partial w} \) — градиент по w. Показывает, как сильно меняется ошибка при изменении \( w \)
- \( \frac{\partial \text{Loss}}{\partial b} \) — градиент по b. Показывает, как сильно меняется ошибка при изменении \( b \)
- \( \alpha \) (альфа) — скорость обучения (learning rate). Размер шага
Знак минус: почему?
Градиент показывает направление роста ошибки. А нам нужно её уменьшить. Поэтому мы идём в противоположную сторону (минус).
Скорость обучения (learning rate)
Параметр \( \alpha \) контролирует размер шага:
Слишком большая скорость (\( \alpha = 1 \)):
- Делаем огромные шаги
- Можем «перепрыгнуть» через минимум
- Ошибка может даже расти!
Слишком маленькая скорость (\( \alpha = 0.001 \)):
- Делаем крошечные шаги
- Очень медленно приближаемся к минимуму
- Нужно много итераций
Оптимально: \( \alpha = 0.01 \) или \( \alpha = 0.1 \) — золотая середина.
Градиенты для логистической регрессии (упрощённо)
Для логистической регрессии с одним признаком градиенты считаются так:
\[ \frac{\partial \text{Loss}}{\partial w} = \frac{1}{n} \sum_{i=1}^{n} (p_i - y_i) \cdot x_i \]
\[ \frac{\partial \text{Loss}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (p_i - y_i) \]
где:
- \( p_i \) — предсказанная вероятность для \( i \)-го примера
- \( y_i \) — правильный класс для \( i \)-го примера
- \( x_i \) — значение признака для \( i \)-го примера
- \( n \) — количество примеров
Интуиция формул
Для градиента по w:
- \( (p_i - y_i) \) — насколько мы ошиблись
- Умножаем на \( x_i \), потому что \( w \) стоит перед признаком
- Усредняем по всем примерам
Для градиента по b:
- Просто средняя ошибка предсказаний
- \( b \) не зависит от признаков, поэтому не умножаем на \( x_i \)
Алгоритм градиентного спуска (пошагово)
1. Инициализация:
w = 0
b = 0
alpha = 0.1 # скорость обучения
epochs = 1000 # количество итераций
2. Повторить epochs раз:
а) Вычислить предсказания:
z = w * X + b
p = sigmoid(z)
б) Вычислить градиенты:
grad_w = mean((p - y) * X)
grad_b = mean(p - y)
в) Обновить параметры:
w = w - alpha * grad_w
b = b - alpha * grad_b
г) (Опционально) Вычислить и вывести ошибку
3. Вернуть w и b
Визуальное представление
Представьте график ошибки:
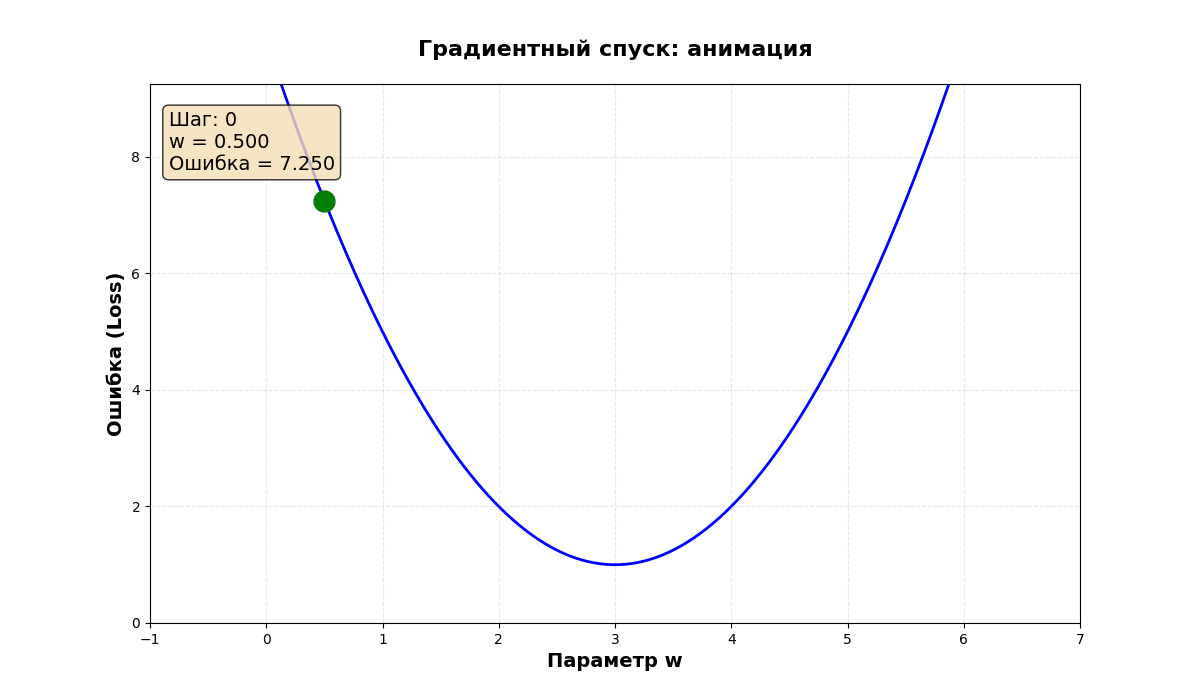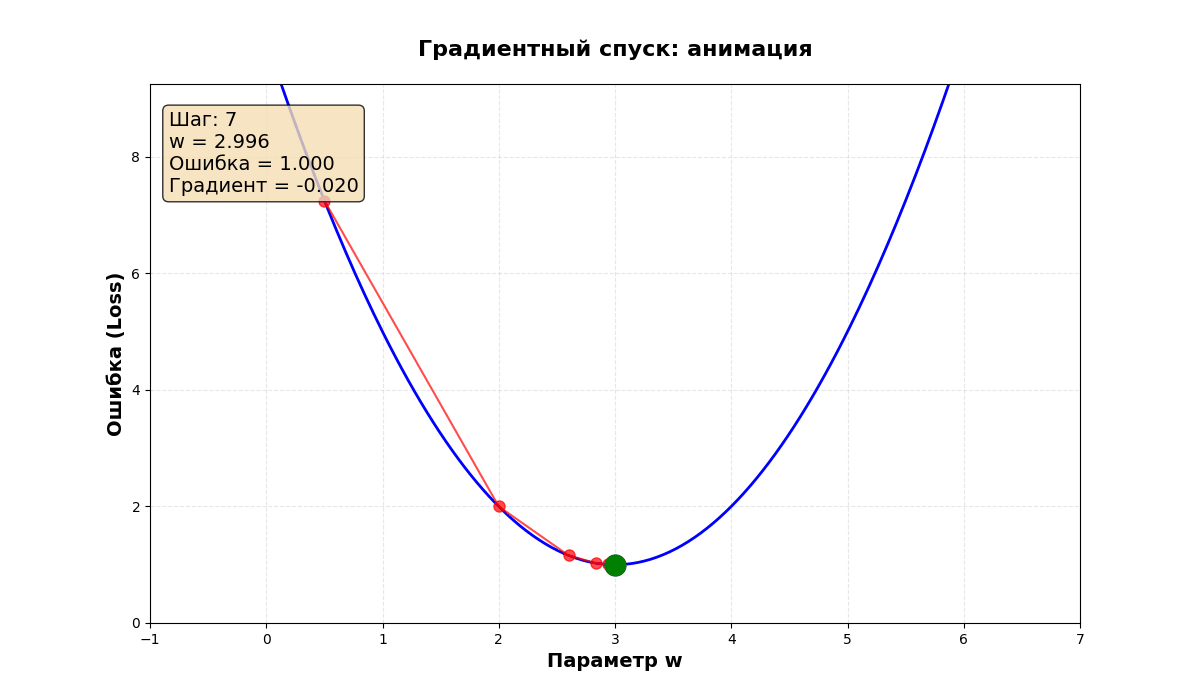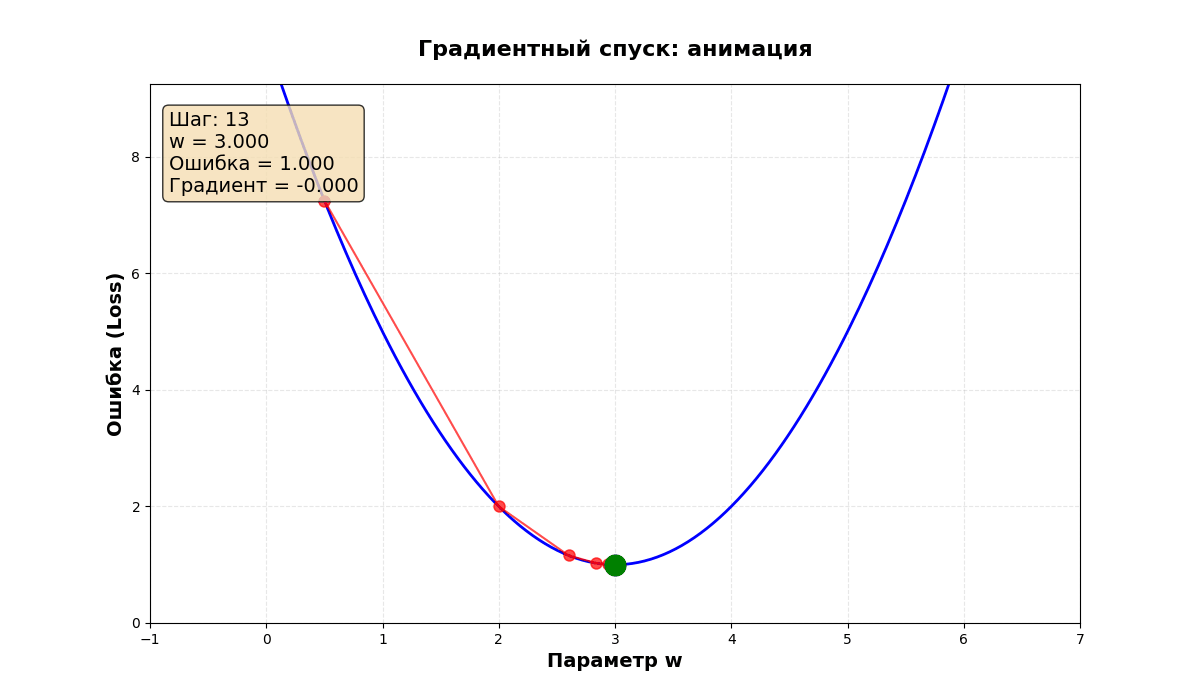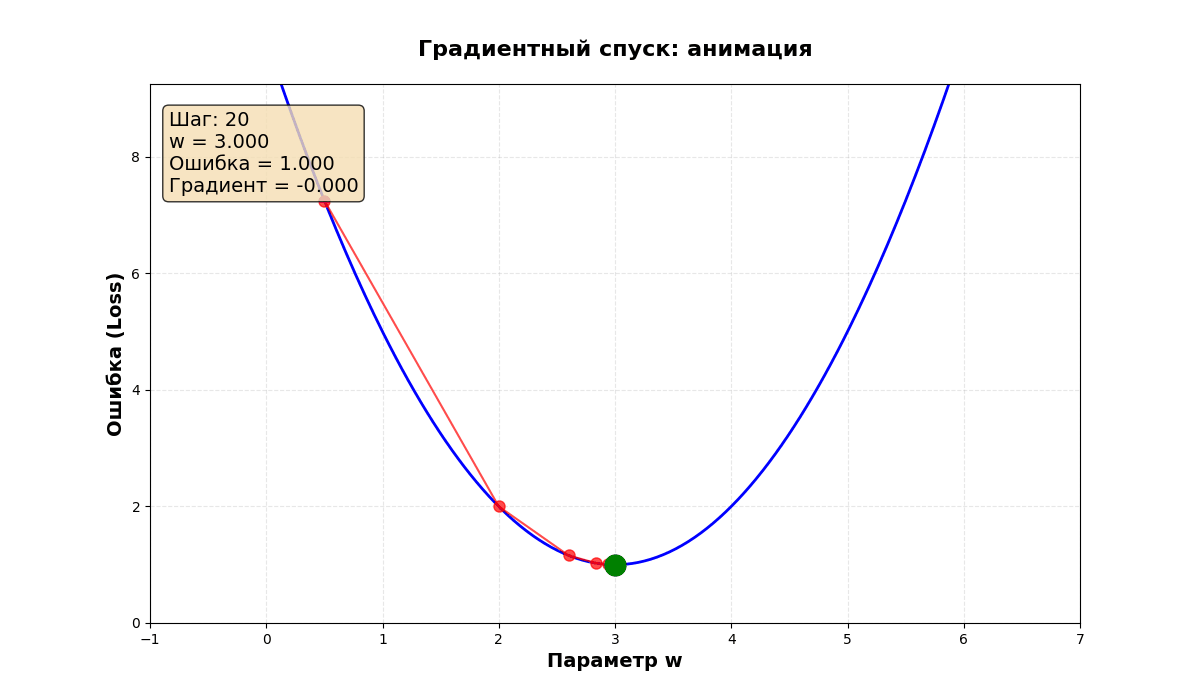
Градиентный спуск:
- Начинает с точки ● (случайное место)
- Каждый шаг двигается вниз по склону
- Останавливается в точке ★ (минимум)
Когда остановиться?
Градиентный спуск обычно останавливают:
- По количеству итераций: Сделали 1000 шагов — хватит
- По изменению ошибки: Если ошибка почти не меняется (например, < 0.0001), значит пришли к минимуму
- По изменению параметров: Если \( w \) и \( b \) почти не меняются
Преимущества градиентного спуска
- Быстро: Не нужно перебирать все варианты
- Масштабируется: Работает для любого количества признаков
- Точно: Находит очень близкое к оптимальному решение
Недостатки
- Может застрять в локальном минимуме (но для логистической регрессии это не проблема — у неё один минимум)
- Требует подбора скорости обучения
- Нужно нормализовать признаки для лучшей работы
Пример: один шаг градиентного спуска
Допустим:
- \( w = 0 \), \( b = 0 \)
- \( X = [36.6, 38.5] \), \( y = [0, 1] \)
- \( \alpha = 0.1 \)
Шаг 1: Вычисляем предсказания
- \( z = [0, 0] \)
- \( p = [0.5, 0.5] \) (сигмоида от нуля)
Шаг 2: Вычисляем градиенты
\[ \text{grad}_w = \frac{1}{2}((0.5-0) \cdot 36.6 + (0.5-1) \cdot 38.5) = \frac{1}{2}(18.3 - 19.25) = -0.475 \]
\[ \text{grad}_b = \frac{1}{2}((0.5-0) + (0.5-1)) = \frac{1}{2}(0.5 - 0.5) = 0 \]
Шаг 3: Обновляем параметры
\[ w = 0 - 0.1 \cdot (-0.475) = 0.0475 \]
\[ b = 0 - 0.1 \cdot 0 = 0 \]
После одного шага \( w \) стало положительным — правильное направление!
Главное
- Градиентный спуск — это умный поиск минимума ошибки
- Вместо перебора всех вариантов мы делаем шаги в направлении уменьшения ошибки
- Градиент показывает направление, скорость обучения — размер шага
- Повторяем много раз, пока не найдём хорошие параметры
- Это основной метод обучения в машинном обучении!
В следующих упражнениях вы сами напишете градиентный спуск и увидите, как он работает!