Вспомним линейную регрессию
Вы уже знаете линейную регрессию: она предсказывает непрерывные числовые значения, такие как цена квартиры, температура или оценка за контрольную.
Модель имеет вид прямой линии:
\(y=w⋅x+b\)
Эта прямая может принимать любые значения на числовой оси: от минус бесконечности до плюс бесконечности.
Пример: Если x — площадь квартиры, то y — её цена в миллионах рублей. Значения могут быть 2.5, 10.8, 150 и так далее.
Новая задача: классификация
Теперь представьте другую задачу: нужно определить, болен человек или здоров, зная его температуру.
Здесь ответ не число, а класс:
Это называется бинарной классификацией.
Вопрос: Можем ли мы использовать линейную регрессию для этой задачи?
Попытка применить линейную регрессию
Попробуем применить линейную регрессию к температуре.
Пусть у нас есть данные:
- 35.5°C → здоров (0)
- 36.0°C → здоров (0)
- 37.0°C → болен (1)
- 38.0°C → болен (1)
Прямая линия даст нам предсказания типа:
- При 34°C → −0.3
- При 35°C → 0.1
- При 37°C → 0.8
- При 40°C → 1.5
Проблема: Что означает −0.3 или 1.5? Это не вероятность! Вероятность должна быть от 0 до 1.
Почему нам нужна вероятность?
В реальной жизни врач не просто говорит «болен» или «здоров», он говорит:
- «С вероятностью 90% он болен»
- «С вероятностью 20% это просто усталость»
Линейная регрессия не может дать нам такую уверенность, потому что её выход — это число не ограничено и может принимать любые значения от −∞ до +∞. Однако для задачи классификации нам нужна вероятность принадлежности объекта к классу 1, то есть число от 0 до 1.
Что нам нужно вместо прямой?
Нам нужна модель, которая:
- Выдаёт вероятность от 0 до 1
- Плавно переходит от «точно класс 0» к «точно класс 1»
- Позволяет настроить порог решения (например, считать больным, если вероятность > 0.5)
Решение: Вместо прямой линии использовать S‑образную кривую (сигмоиду), которая «сжимает» любые значения в диапазон от 0 до 1.
Сигмоида
Сигмоида (или логистическая функция) выглядит так:
\(p = \sigma(z) = \frac{1}{1+e^{-z}}\)
Где \(z=w⋅x+b\)
Свойства сигмоиды:
- Если z очень большое положительное число → p близко к 1
- Если z очень большое отрицательное число → p близко к 0
- Если z=0 → p=0.5 (граница между классами)
График сигмоиды:
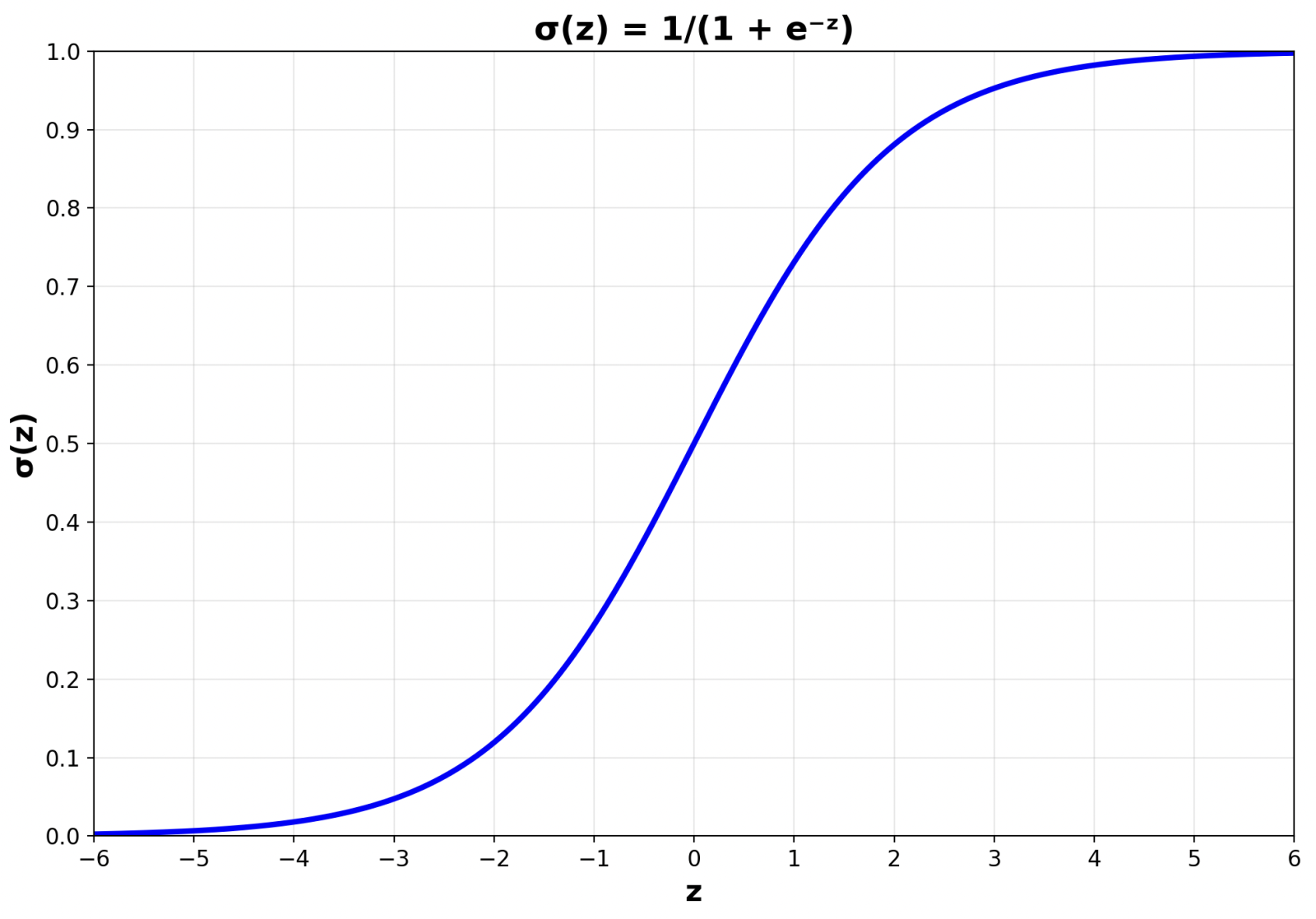
Вы видите S‑образную кривую? Она плавно переходит от 0 к 1, никогда не выходя за эти границы.
Что такое z и почему это важно?
Число z — это результат линейной комбинации признаков. Его ещё называют логитом.
Представьте z как «сырую оценку» модели:
- Если z > 0 — модель склоняется к классу 1 (болен)
- Если z < 0 — модель склоняется к классу 0 (здоров)
- Если z = 0 — модель не уверена (50% на 50%)
Сигмоида преобразует эту «сырую оценку» в понятную вероятность.
Как это работает на примере температуры
Пусть наша модель нашла параметры w=2, b=−74.
Тогда для температуры x=37:
z = 2⋅37−74 = 0
p = σ(0) = 0.5
Вероятность болезни = 50%
Для x=38:
z=2⋅38−74=2
p=σ(2)≈0.88
Вероятность болезни = 88%
Для x=36:
z=2⋅36−74=−2
p=σ(−2)≈0.12
Вероятность болезни = 12%
Теперь у нас есть осмысленные вероятности для каждой температуры !
От вероятности к классу: порог принятия решения
Когда у нас есть вероятность p, мы можем превратить её в класс, используя порог τ (обычно τ=0.5):
\(\text{Класс} = \begin{cases} 1 & \text{если } p \ge 0.5 \\ 0 & \text{если } p < 0.5 \end{cases} \)
Пример:
- p=0.88 → Класс = 1 (болен)
- p=0.12 → Класс = 0 (здоров)
- p=0.50 → Класс = 1 (граница)
Можно ли менять порог?
Да! Порог не обязательно должен быть 0.5. Его можно менять в зависимости от задачи:
- Порог = 0.3: Модель будет чаще говорить «болен». Это полезно, если пропустить болезнь опаснее, чем лишний раз отправить на анализ.
- Порог = 0.7: Модель будет осторожнее и говорить «болен» только при высокой уверенности.
Выбор порога — это баланс между двумя типами ошибок: пропустить больного или ложно обеспокоить здорового.
Граница решения: линия, разделяющая классы
Несмотря на S‑образную кривую сигмоиды, в пространстве признаков граница решений остаётся линейной.
Для одного признака: граница — это точка (где z=0)
Для двух признаков: граница — это прямая
Для трёх признаков: граница — это плоскость
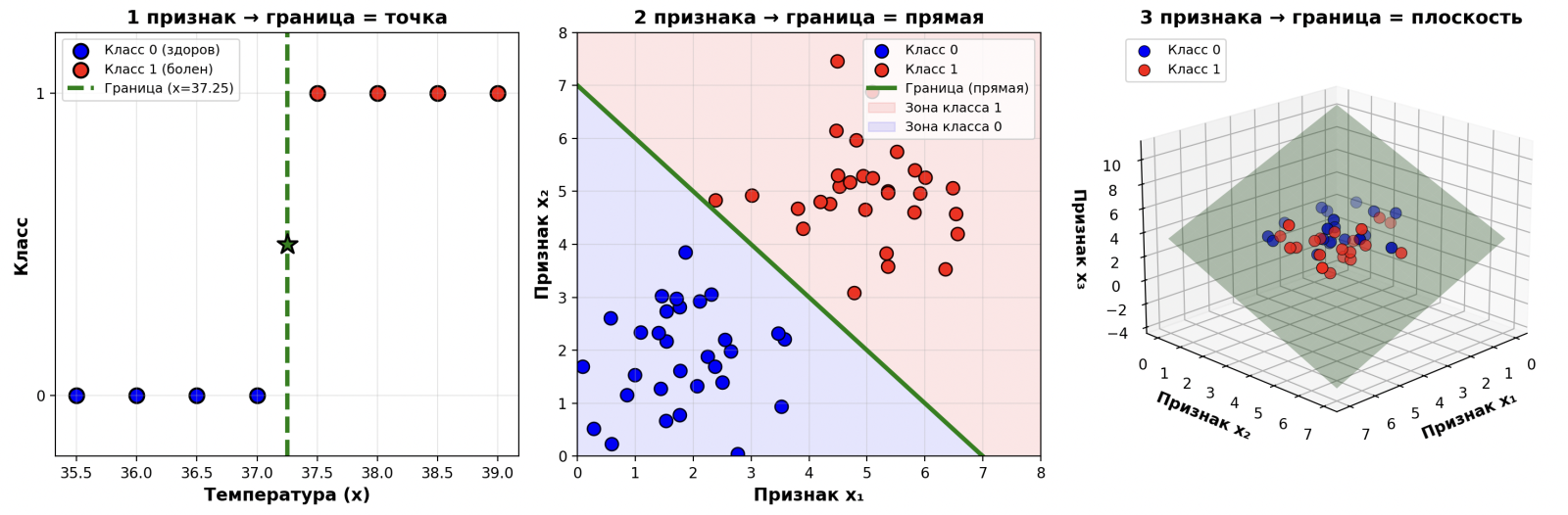
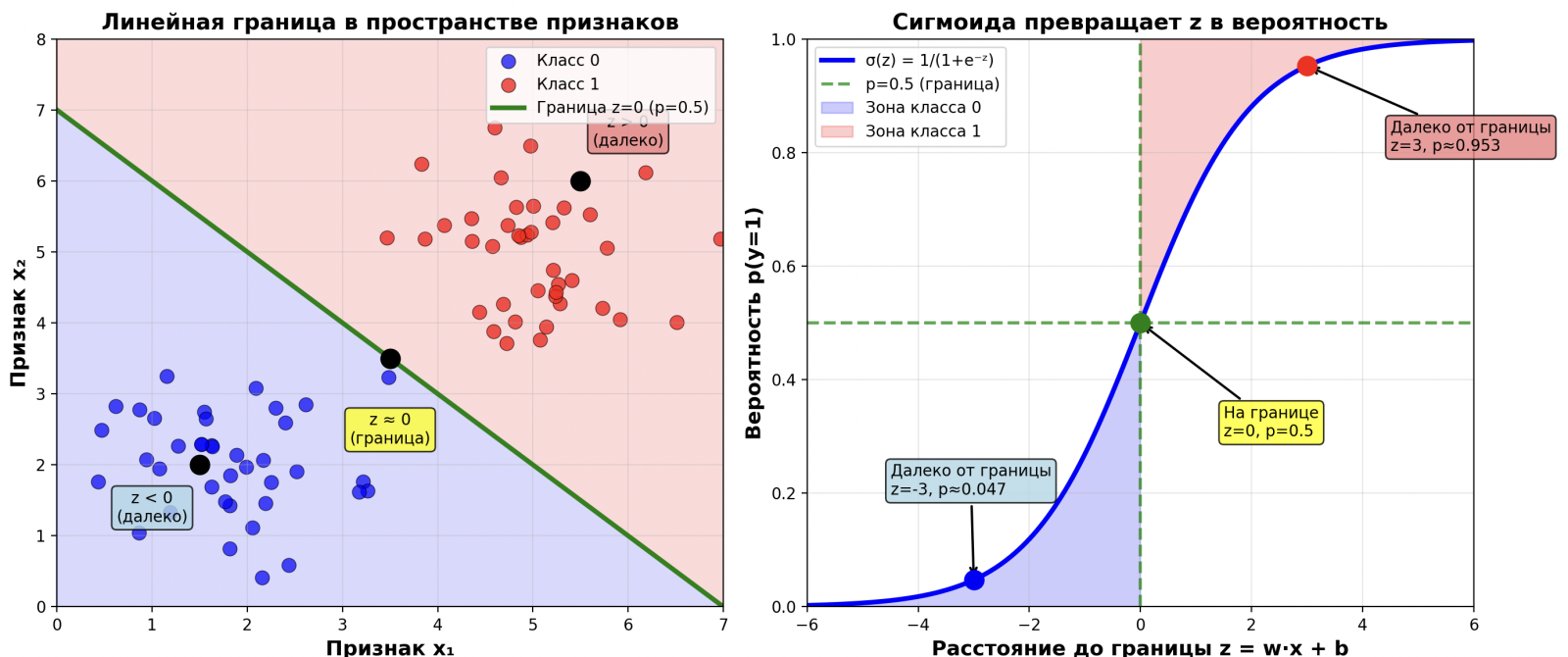
На графике видно: модель разделяет классы прямой линией (или плоскостью), но превращает расстояние до этой линии в вероятность через сигмоиду.
Логит: связь между вероятностью и z
Если у нас есть вероятность p, мы можем вернуться к z через логит-функцию:
logit(p) = log(p/(1-p)) = z
Это показывает, что z — это логарифм шансов (odds). Шансы — это отношение вероятности «быть в классе 1» к вероятности «быть в классе 0».
Пример:
- Если p = 0.8, то шансы = 0.8/0.2 = 4 (в 4 раза вероятнее быть больным, чем здоровым)
- logit(0.8) ≈ 1.39
А нельзя ли просто округлить линейную регрессию?
Можно попробовать: взять линейную регрессию, получить предсказание и округлить его до 0 или 1.
Проблемы:
- На краях данных модель даст абсурдные значения (−5, 10), которые после округления всё равно дадут неверный класс
- Нет вероятностей — нельзя понять уверенность модели
- Модель не оптимизирована под задачу классификации: она минимизирует ошибку предсказания числа, а не вероятности класса
Подведём итог
- Линейная регрессия предсказывает числа без ограничений.
- Логистическая регрессия предсказывает вероятности от 0 до 1 с помощью сигмоиды.
- Сигмоида превращает любое число z в вероятность p.
- Мы выбираем порог (обычно 0.5), чтобы превратить вероятность в класс.
- Граница между классами остаётся линейной, но сигмоида показывает уверенность модели.
Сравнение: линейная vs логистическая регрессия
| Критерий |
Линейная регрессия |
Логистическая регрессия |
| Задача |
Предсказание числа |
Классификация (да/нет) |
| Выход |
Любое число (−∞, +∞) |
Вероятность |
| График |
Прямая линия |
S‑образная кривая |
| Распределение |
Нормальное (гауссово) |
Биномиальное |
| Функция потерь |
MSE (средний квадрат ошибки) |
Log‑loss (кросс‑энтропия) |
| Пример |
Цена квартиры, оценка за тест |
Спам/не спам, болен/здоров |
Визуализация: код для построения графика сигмоиды
Вы можете построить график сигмоиды самостоятельно в Python