|
Рассмотрим такую задачу: какое наибольшее число ферзей можно поставить на доску 8×8 так, чтобы никакие 2 ферзя не били друг друга?
Выберите все верные рассуждения (не обязательно приводящие к оптимальному ответу).
Напоминание. Ферзь ходит на любое количество клеток по вертикали, горизонтали или диагонали.
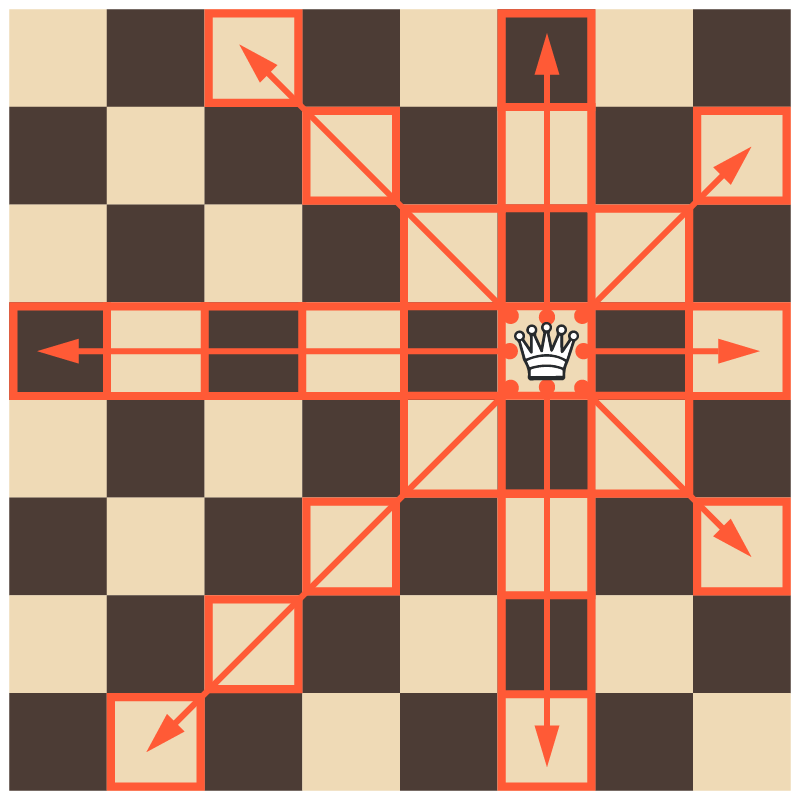
| 1 |
Разобьём доску на 15 диагоналей, «идущих в одном направлении» (включая диагонали, состоящие из одной клетки). На каждой из них стоит не больше одного ферзя, поэтому всего ферзей не больше 15.
 |
| 2 |
Разобьём доску на 8 вертикалей. В каждой вертикали стоит не больше одного ферзя, поэтому всего ферзей не больше 8.
 |
| 3 |
Разобьём доску на 8 горизонталей. В каждой горизонтали может стоять только один ферзь. Следовательно, на доску можно поставить 8 ферзей.
 |
| 4 |
Разобьём доску на 8 вертикалей. В каждой вертикали стоит не больше одного ферзя. Разобьём доску на 8 горизонталей. В каждой горизонтали стоит не больше одного ферзя. Поэтому на доску можно поставить 8 ферзей. |
В качестве ответа введите номера верных утверждений (цифры в строку через пробел в произвольном порядке)
|