Статья Автор: Лебедев Дмитрий

Конспект _Выигрышные и проигрышные позиции


Комби-7 Выигрыщные и проигрышные позиции. Часть 1 Стратегия дополненния 

В некоторых играх можно «дополнять» ходы противника по определённому принципу, поддерживая игру после каждого своего хода в «выгодном» состоянии.

Задача. На столе лежит 200 спичек. Двое по очереди забирают со стола 1, 2, 3 или 4 спички. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Задача. На столе лежит 55 камней. Двое по очереди забирают со стола 1, 4 или 9 камней. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Комби-7 Выигрыщные и проигрышные позиции. Часть 2 Разбиение на пары

В некоторых играх можно разбить объекты игры или позиции на пары и «завершать» пары, затронутые противником. Например, таким образом можно гарантировать себе возможность ходить.

Задача. Имеется таблица размером 2×5 и 10 карточек с числами 1, 2, …, 10. Двое по очереди выкладывают эти карточки на клетки таблицы. После того как все карточки выложены, в каждом из пяти столбцов находится наименьшее число, и все эти наименьшие числа складываются. Если полученная сумма делится на 10, то выигрывает второй игрок, а если не делится — то первый. Кто выигрывает при правильной игре?

Задача. Есть шахматная доска, на некоторой клетке которой стоит король. Двое по очереди делают королём ходы, причём нельзя делать ход в клетку, в которой король уже был. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Комби-7 Выигрыщные и проигрышные позиции. Часть 3 Стратегия принуждения 

Задача. В левом нижнем углу шахматной доски стоит ладья. За один ход разрешается сдвинуть её на любое количество клеток вверх или любое количество клеток вправо. Двое по очереди двигают ладью до тех пор, пока какой-то игрок не сможет сделать ход. Этот игрок считается проигравшим. Кто выигрывает при правильной игре?

Задача. Есть прямоугольник 7×10, составленный из точек. Двое игроков по очереди соединяют соседние узлы отрезками: первый игрок соединяет узлы по диагонали, а второй — по вертикали или по горизонтали. Ломаная, полученная к концу игры, должна быть несамопересекающейся. Они начинают из левой нижней точки. Выигрывает тот, кто проведёт отрезок в правую верхнюю точку. Сможет ли кто-то гарантированно добиться победы, и если сможет, то кто именно?

Комби-7 Выигрыщные и проигрышные позиции. Часть 4. Анализ позиций 

Позиция — это текущее состояние в игре. Позиция называется выигрышной, если игрок, делающий ход из этой позиции, может обеспечить себе победу. В противном случае позиция называется проигрышной.

Правила заполнения позиций:

  • позиция, из которой нельзя сделать ход, — проигрышная;
  • если из позиции X можно попасть в проигрышную позицию, то X — выигрышная;
  • если все ходы из позиции X ведут в выигрышные позиции, то X — проигрышная.

Задача. На столе лежит 7 камней. Двое по очереди забирают со стола 1, 2 или 4 камня. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Задачи для тренировки

1) 7_17_1 На столе лежит N спичек

  
2)  7_17_2 На столе лежит N спичек  
3) 7_17_3  Задача про купюры  
4) 7_17_4 На экране калькулятора горит число 1234   
5) 7_17_5 На доске написаны числа 1, 2,…,…,14.  
6) 7_17_6 В ряд выписаны, чередуясь, 100 двоек и 99 единиц  
7) 7_17_7 На доске 8×7 в левом нижнем углу стоит слон  
8) 7_17_8 На доске 8×7 стоит слон (на b1)  
9) 7_17_9 На столе лежит несколько камней  
10) 7_17_10 На столе лежит несколько камней  
11) 7_17_11 В левом нижнем углу доски 4×4 стоит ладья  
12) 7_17_12 В левом нижнем углу доски 6×4 стоит ферзь  

Задачи с разбором

Разбор 1 "На столе лежит куча из 555 спичек"
Задача 1. На столе лежит куча из 555 спичек. Двое играют в такую игру: за один ход начинающий может взять 1, 2, 3 или 4 спички, а второй игрок — 1, 2, 3 спички или пропустить ход. Выигрывает тот, кто берёт последнюю спичку. Кто выиграет при правильной игре?  
Разбор 2 "Двое по очереди вписывают "
Задача 2. Двое по очереди вписывают в клетки таблицы 7×7 цифры 1, 2, …, 7. Нельзя ходить так, чтобы в одной строке или в одном столбце оказались одинаковые цифры. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?  
Разбор 3 "Петя и Вася играют на доске 20*20"

Задача 3. Петя и Вася играют на доске 20×20. Петя может за ход вырезать одну клетку, а Вася — трёхклеточный уголок.

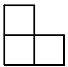
Начинает Петя. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

  
Разбор 4a "Задача про 30-значное число"
Задача 4a. Двое пишут 30-значное число, используя цифры 1, 2, 3, 4, 5. Первую цифру пишет первый, вторую — второй, третью — первый и т. д. Может ли второй добиться того, чтобы полученное число разделилось на 9, если первый стремится ему помешать?  
Разбор 4b "Задача про 20-значное число"
Задача 4b. Двое пишут 20-значное число, используя цифры 1, 2, 3, 4, 5. Первую цифру пишет первый, вторую — второй, третью — первый и т. д. Может ли второй добиться того, чтобы полученное число разделилось на 9, если первый стремится ему помешать?  
Разбор 5 "По кругу расставлены 50 фишек "
Задача 5. По кругу расставлены 50 фишек. Двое по очереди берут по три фишки каждый. Первый игрок хочет, чтобы в конце остались две фишки, не лежащие рядом. Может ли второй ему помешать?  
Разбор 6 "Петя и Вася разложили на столе 13 различных карт"

Задача 6. Петя и Вася разложили на столе 13 различных карт. Каждая карта может лежать в одном из двух положений: рубашкой вверх или рубашкой вниз. Изначально карты лежат произвольным образом. Игроки должны по очереди переворачивать по одной карте. Проигрывает тот игрок, после хода которого повторится какая-то из предыдущих ситуаций (включая изначальную). Первый ход сделал Петя. Кто выиграет при правильной игре?

Пример расположения карт:

  
Разбор 7 "В левом нижнем углу доски стоит король "

Задача 7. В левом нижнем углу доски стоит король. Двое игроков по очереди сдвигают его на одну клетку вправо, вверх или по диагонали. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

  
Разбор 8 "Задача про игру с числом 4"

Задача 8. На доске написано число 4. Двое по очереди добавляют к нему натуральное число, меньшее текущего числа на доске. Выигрывает тот, после чьего хода на доске появится число 100. Кто выиграет при правильной игре?

  
Разбор 9 "Задача про часы"

Задача 9. Есть часы с одной стрелкой, которая изначально показывает на деление 11. Двое игроков по очереди сдвигают стрелку на два или три деления вперёд по часовой стрелке. Побеждает тот, после чьего хода стрелка будет показывать на деление 1212. Кто сможет выиграть при правильной игре?

  

Печать