Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 10) ИЛИ ((х < 9) И (x >= 8))
🔹 1. Разберём высказывание по частям
Последняя операция, которая будет выполняться в данном высказывании - это операция ИЛИ. Следовательно, у нас есть сложное условие, состоящее из двух частей, соединённых ИЛИ:
-
НЕ (x < 10)
-
(x < 9) И (x >= 8)
Нам нужно найти наибольшее натуральное x, при котором всё высказывание ложно.
🔹 2. Когда "ИЛИ" ложно?
Высказывание A ИЛИ B ложно только если ложны и A и B одновременно.
Значит, нам нужно, чтобы:
-
НЕ (x < 10) = ложь
-
(x < 9) И (x >= 8) = ложь
🔹 3. Разбираем первое условие: НЕ (x < 10) = ложь
Вывод первый: x может быть 1, 2, 3, ..., 9.
🔹 4. Разбираем второе условие: (x < 9) И (x >= 8) = ложь
Это условие ложно, если хотя бы одна часть ложна:
-
x < 9 = ложь → x ≥ 9
-
Тогда x может быть 9, 10, 11, ...
-
Но из Шага 3 x<10, значит, остаётся только 9.
-
x >= 8 = ложь → x < 8
Вывод второй:
-
Если x = 9, условие (x < 9) И (x >= 8) = ложь (потому что x < 9 ложно).
-
Если x = 8, условие (x < 9) И (x >= 8) = истина (оба верны).
-
Если x ≤ 7, условие ложь (потому что x >= 8 ложно).
🔹 5. Объединяем оба условия
Нам нужно, чтобы:
-
x<10 (из Шага 3),
-
(x < 9) И (x >= 8) = ложь.
Рассмотрим возможные x:
🔹 Шаг 6. Выбираем наибольшее подходящее число
Из подходящих вариантов (9,7,6,…) наибольшее — это 9.
✅ Ответ: x=9
🔹 Проверка:
Подставим x = 9:
НЕ (9 < 10) ИЛИ ((9 < 9) И (9 >= 8)) = НЕ (истина) ИЛИ (ложь И истина) = ложь ИЛИ ложь = ложь
Всё верно!
Решение данной задачи можно оформить на числовой оси
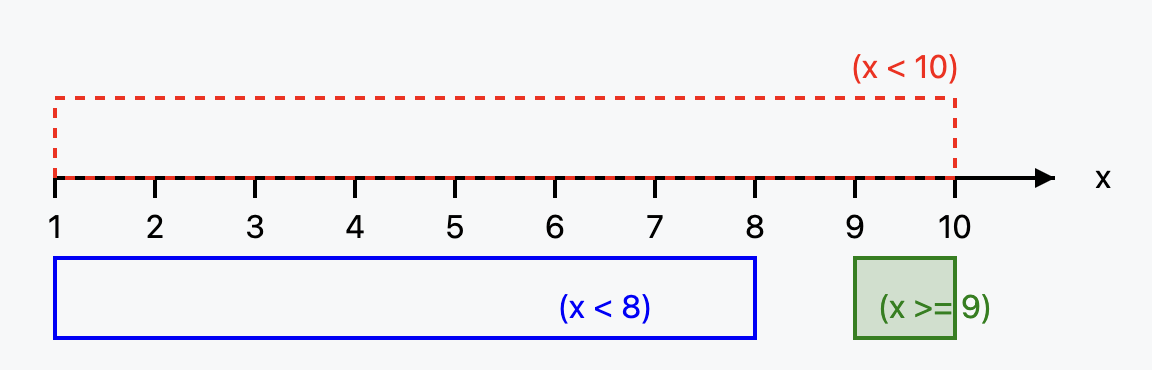
Подходящие числа находятся на пересечении красной области с синей и зеленой, То есть под наш ответ подходят числа [1; 7] и [9]. Наибольшее из них - это число 9.